淺談電磁波

電磁波是甚麼？電磁波是以什麼樣的型態存在於這個世界中？

這幾個問題過去一直讓我感到十分困惑，最近和文于學長經過了兩個晚上的討論後才終於有了比較精確的想法，因為太興奮了決定在這邊分享給大家。

首先，先來回顧一下真空中 Maxwell 方程組的型式：

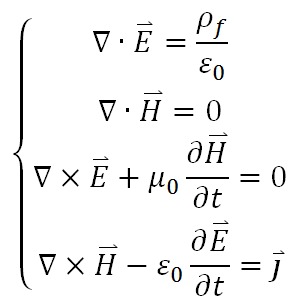
要考慮電磁波，就得先考慮電磁波存在之處有著什麼樣的條件。最理想的情況是，我們希望電磁場區沒有任何電荷和電流，並去了解在這樣的場區下電磁場會有什麼樣的行為。於是在這樣的場區條件下，剛才的方程會變成以下的聯立型式：

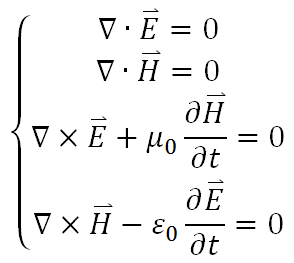
這個時候，我們可以輕易看出電場和磁場的特質，以及兩者之間的交互作用。值得注意的是，電場散度為零是因為場區沒有電荷，磁場散度為零是因為世界不存在磁單極，雖然其微分方程的形式一樣，但物理意義上是不一樣的。接下來，我們想要單就電場和磁場的性質來討論，於是我們可以將聯立方程帶入重組後化為更簡便的型式：

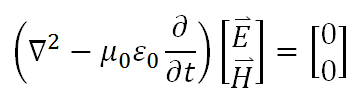
上面的這個微分方程被稱做 Maxwell 的波動方程，在一般的電磁學書中，它們給出了這個波動方程的通解如下：

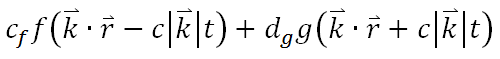
現在來思考一下這個通解的意義。以通解的第一項來說，如果它的值是個常數，則裡面的自變數一定也會是個常數：

這個函數的自變數是常數有何意義呢？從幾何的角度來看，如果鎖定一個特定的「時刻 t」，此時自變數的後項也變常數了。原本的 k 是個常數向量，所有滿足和 k內積為常數的位置向量端點必然會構成一個與 k 垂直的平面。因此我們可以知道在某一個時刻t時，函數f的等相面會是個平面，而當時間在流逝（也就是 t 在增加）時，位置向量與k的內積值亦會增加，換句話說就是整個平面會朝 k 方向前進，我們把滿足這種現象的函數稱做「平面波」。

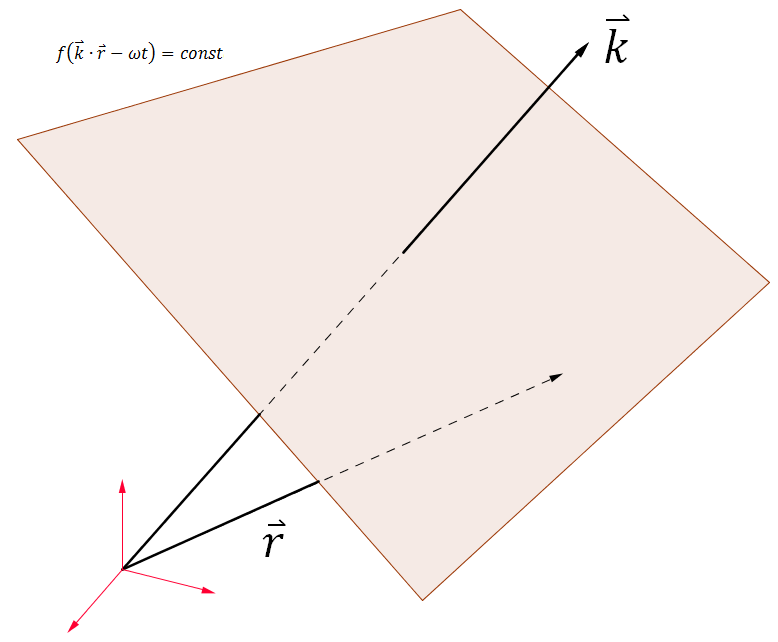
因為現在考慮的被微分項是電場和磁場，兩者都是向量函數，也就是說這個通解 f 會是個向量函數。一般的純量函數，例如溫度場，代表著空間中選取任何一個點，都會在該點感應到一個溫度值；而向量函數則代表著空間中選取任何一個點，都會感應到一個向量值。以電場來看的話，我在空間中不管選取哪一個點，都會感受到該點有個相應之電場向量，如果把電荷放上那個點，電荷就會感受到一股力在拉它。
現在我們探討一下電場的等相面的意義。剛剛說過，f 是常數值時，所有滿足 f 是常數的位置會是與 k 方向垂直的一個無限大平面，這個平面被我們稱做等相面。今天的 f 是電場（或磁場），便意味著在它的等相面上每一點，電場（或磁場）都會相同，而當我們沿著k方向選取不同的等相面時，不同等相面上的電場（或磁場）就會不同。現在考慮一個平面波如下：

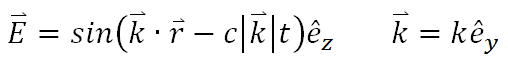
這個平面波代表著我任取一個與 k 方向垂直的平面，這個平面上每一點的電場值都固定。但我取不同平面來比對上面的電場值，會發向這些值隨著選取平面沿著k方向增加，會是一個 sin 的函數。畫成圖會長得像下面這張一樣（注意，圖中的面上每一點都有著相同的電場值，這邊為求方便僅在第一個面多畫幾個點的電場來示意）

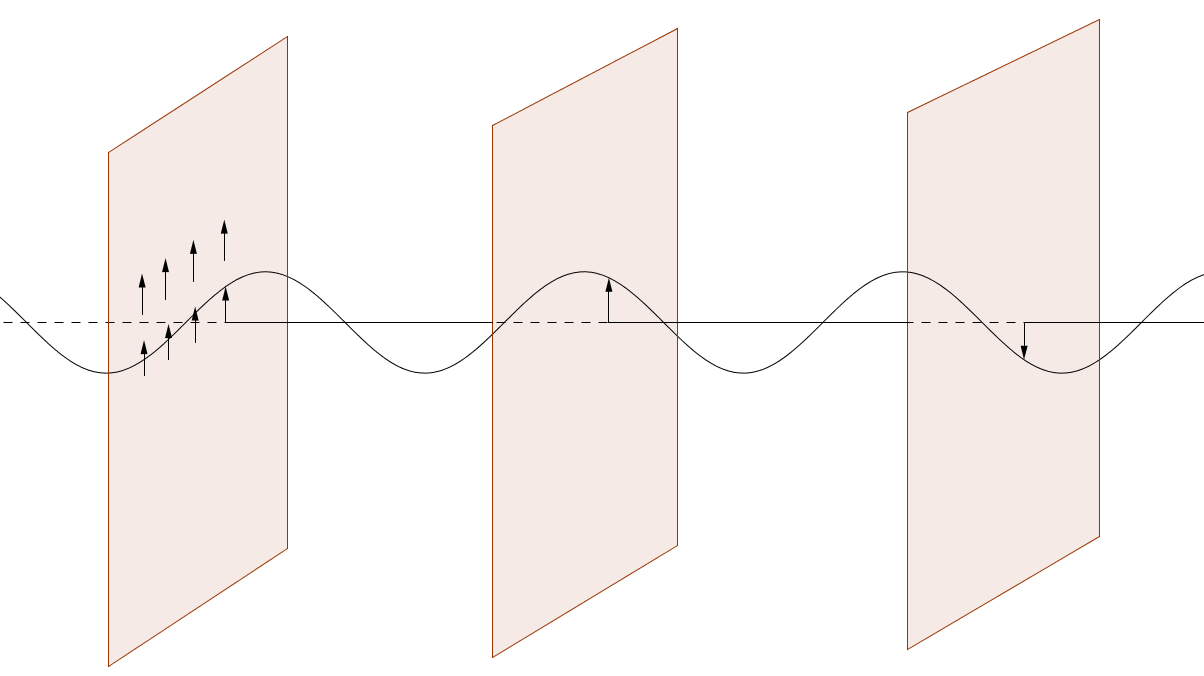
現在如果我選取一個跟 k 方向同向的軸，這個軸會穿越所有的平面，軸上每個點都會有一個對應的電場向量。同樣的考慮磁場，軸上的每個點也會有對應到一個磁場向量。如果我們把所有點對應到的電場向量和磁場向量畫在點上，就會變成科普書和教科書很常看到的電磁波圖。

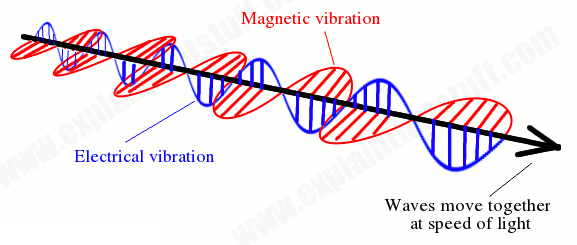
很多人會誤以為，電磁波是一束這樣的東西在空間中跑來跑去，這樣的想法是錯誤的。正確的想法是，空間中每一點都有電場和磁場，這些電磁場的大小方向會隨時間改變，而物理學家為了要了解它們跟時間的關係，於是發展出電磁波的概念來解釋，這張圖給我們看到的只是沿著電磁波行進方向上的某條直線上每一點的電場和磁場，而不是「一個電磁波」。

接下來要提的這點非常重要。我重新列一次剛剛所列過的 Maxwell 波動方程：

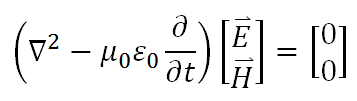
這個方程在沒有電荷和電流的地方是恆成立的。接著你可能會想，靜電場和靜磁場明明就不是電磁波阿，為甚麼會滿足波動方程呢？這個想法其實很簡單，因為靜電場和靜磁場跟時間 t 這個參數無關，所以對t的偏微分一定等於零。然後在沒有電荷和電流處，它們的 laplacian 也一定是零，所以靜電場和靜磁場並沒有違背波動方程。你可以把它們想成一個「沒有在震盪的波」，這就解釋了為靜電磁場甚麼依然滿足波動方程。

很神奇的一點是，只要是時變的電磁場，任一點的電場和磁場一定垂直，兩者的外積必為電磁波行進的方向，而電磁波行進的速度必為光速，這些神奇的結論大大的影響了近代物理的發展，也在日後被證實光即是電磁波。這些性質在電磁學和近代物理的書都已被廣泛討論，此處不多做贅述。

接下來讓我們來釐清一下幾件事情。首先：為甚麼大部分書中討論的電磁波都是正弦波呢？這並不是因為大自然中的電磁波都是正弦波，而是因為由傅立葉轉換可以知道，所有的波形都可以視為無限種不同頻率的弦波疊加，疊加的公式如下。式子左邊是任意的波形函數，右邊則是任意波長的弦波乘上對應的權重後做積分，弦波函數的完備性告訴我們一定存在一種特定的疊加權重可以把無限多種弦波疊加成任意波形。

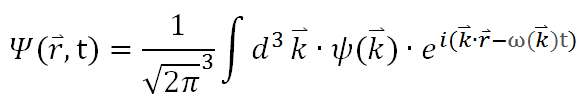
這件事情告訴我們：只要能掌握弦波的性質，便就能掌握任何一種電磁波的性質，因為我們只要把它們拆解成弦波來討論就好了。

再來讓我們釐清一下甚麼是波動方程是的「通解」。我在前面曾給出一般電磁學課本所提到的波動方程「通解」如下，並稱其為平面波：

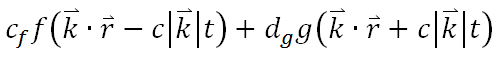
其實這個講法有些不妥。自然界中的電磁波是由許多平面波疊加而成的，而這些朝著不同方向行進的平面波在經過疊加後可能以其他的型式存在，諸如球面波等。可是等等，球面波不就不再是平面波了嗎？這樣難道不會跟我們原本所給的「通解」自相矛盾嗎？

於是我們發現，原本給的並不能算是「通解」，只能說電磁波是由許多這種形式的平面波所疊加的，然而每個平面波的k向量都不同，疊加後自然不再是平面波。真正的通解應該寫成以下型式：

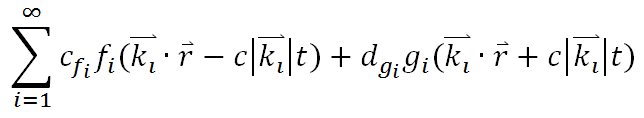
這樣我們就得到一個對電磁波完備的數學描述了：所有的電磁波都可視為由無限種不同的平面波疊加而成。

最後讓我們來思考一下愛因斯坦著名的「追光實驗」。在愛因斯坦提出相對論之前，他曾用伽利略的座標轉換來思考一件事情：如果我用光速在追逐一道光，那 Maxwell 的電磁學定律還會成立嗎？

假設伽利略的座標轉換是正確的，那現在來考慮剛才作為例子的正弦電磁波。我對這個電磁波選取一個面，這個面和所有的電場方向平行，和所有的磁場方向垂直。如果我在這個面上選取一個長方形區域，並將電場沿著這個長方形區域做環積分，你會發現一件事情：這個環積分不等於零。原因是長方形左右兩個邊線上的電場值不同，所以積出來會有差值。於是我們得到了下面這條式子：

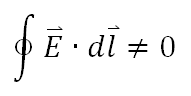
接下來考慮磁場對這個長方形的面積分，你會發現因為你用光速追著光在跑，在伽利略的系統下，你會覺得光是靜止的，所以你將感受不到磁場隨時間的變化。換句話說，從你的視野來看磁場是靜止的，於是磁場對這個長方形的面積分將會是個常數，如果將它對時間微分必會得到零。

現在我把第二式乘上磁導率常數再與第一式相加，你會發現：

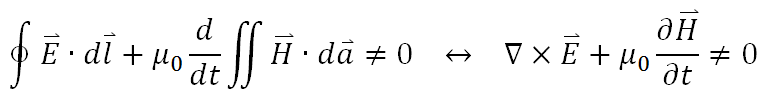
於是，Maxwell 方程的第三條－Faraday 定律便失效了！就是這件事讓愛因斯坦深入去思考空間轉換的本質，並發展出狹義相對論，而那又是另一段故事了。